Alistair
AH fanatic
- Joined
- May 25, 2018
- Messages
- 874
- Reaction score
- 3,091
- Location
- Milwaukee, WI
- Media
- 2
- Articles
- 1
- Hunted
- Scotland, Ireland & England
Hello folks.
I've been meaning to put something together on this topic for a while as it's a persistent blind spot within the shooting and reloading community. @Shooter375 s recent thread on crimping finally gave me the incentive to put words to forum. Not calling him out specifically, just the latest in a long line of threads on reloading, grouping and what it all means. I think this'll be of interest to a few of our members and may spark some lively discussion.
This post will be long, and will be split into 2 main topics:
1. Basic statistics and why 3 round group don't mean anything. This'll be math heavy (dull, I know!), but should be mildly interesting and give sufficient background for it all to make sense.
2. If 3 round groups mean nothing, then what can we do instead to guide load development? This section will be more practical and maybe it'll save people some time and money.
Here we go!
Topic 1 - Stats 'n' stuff.
This is a normal distribution curve:
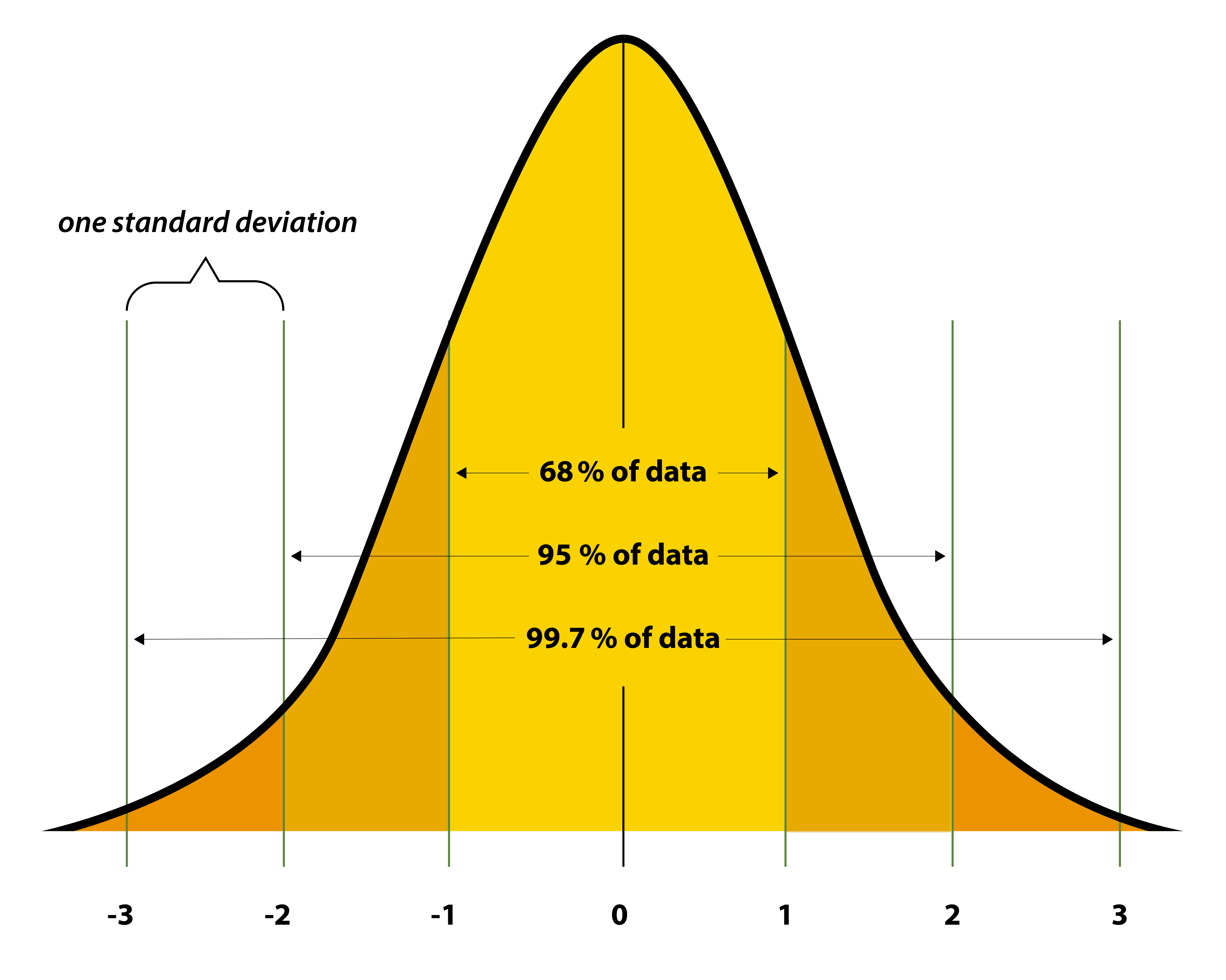
Scary, I know. But it's a surprisingly useful thing. What this curve does, is explain the distribution of data points within a sample using 2 main criteria. These are; the mean of the data set, and the standard deviation (SD). I will not go into the math of what SD is, but this link is here for those who are interested: https://www.mathsisfun.com/data/standard-deviation.html
This calculator allows you to calculate SD from a data set: https://www.calculator.net/standard-deviation-calculator.html
We'll get onto that later. Use 'Sample', not 'Population'.
This curve assumes something called 'normal' or Gaussian distribution. It assumes that data is spread about the mean in a specific way, with no skew to the high end, or the low end. Not all data does this, but normal distribution is called 'normal' for a reason. It is incredibly common in nature, and in complex systems. Examples of data that follow this trend include; height of people within a population, IQ in a population, torque applied to a bolt by a torque wrench, and roughly 90% of all other examples that spring to mind. Some topical ones for us on this forum might include bullet weights within a single box of bullets or velocity of a given load.
The curve actually tells us quite a lot about the data and helps us make conclusions. The mean tells us the mid point, whilst the standard deviation tells us how spread out that data is about the mean. A small SD suggests that all data points are tightly clustered, giving a steeper curve. You'll notice in the above that we have lines at -3, -2, -1, 0 and so forth. Each of these describes one standard deviation, and as the figure shows, we can make clear statements about what percent of our data points fit within a certain number of SDs from the mean.
As an example, Let's say you buy a box of shiny 300gr bullets. You weigh 20 of 'em, stick the values into the calculator above. You find that the mean is 300gr and the SD is 2gr. This tells us that in your box of 100 bullets, 68 of them weigh between 298 and 302gr, 95 of them weigh between 296 and 304gr, and all 100 of them weigh between 294gr and 306gr. 20 bullets (the sample) tells you enough about the entire box (population) to say this with confidence (real, statistical confidence, not the usual bollocks shooters say!)
Cool stuff, but why should you care?
Well, as with most complex systems, the grouping of a given load also follows this normal distribution. That's unsurprising. A rifle and its load is a complex system, made up of a whole lot of variables which themselves follow normal distributions. Bullet weight. Bullet diameter. Neck tension. Case volume. Specific energy of powder. Powder charge. Primer energy. All have a mean that they vary about randomly following the distribution above.
We can therefore imagine the group of a rifle to look something like this if you fired say 1000 rounds:
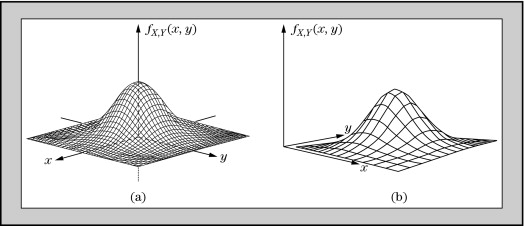
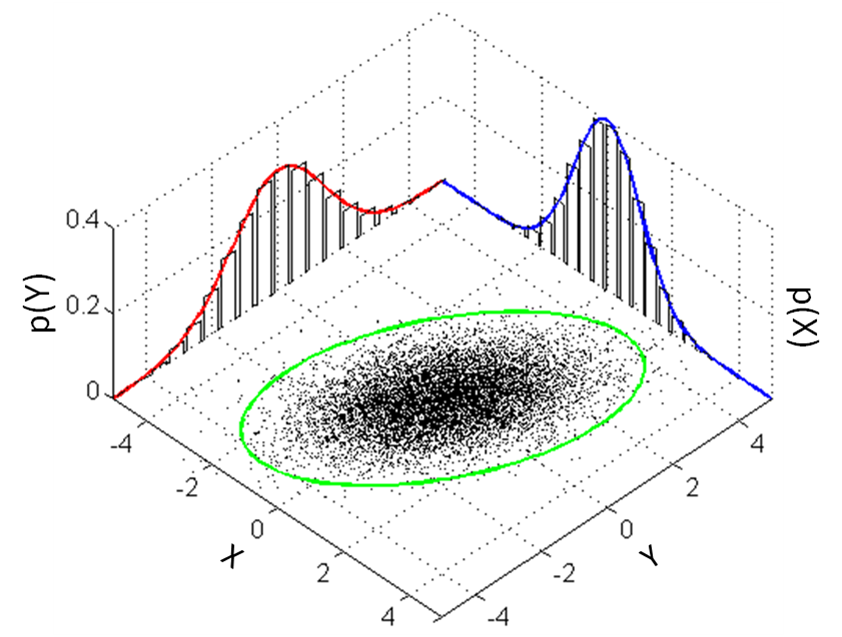
You have a normal distribution for 'x' (horizontal dispersion) and a normal distribution for 'y' (vertical dispersion) with the height of the little hill at any given (x,y) defining the relative number of those 1000 rounds that fall there. The middle of the hill would have coordinates 0,0 as it is 0" away from the center of the group both vertically and horizontally. You'll see that most rounds fall in the middle (mean +/-1 SD) but that some rounds fall further from the center at 2 or even 3 SD away from the mean center of the group.
So now you know what your group is doing, but what does it have to do with 3 round groups?
Well, let's say you have 2 loads, both of which have exactly the same mean (0,0) and the same SD (let's say 0.5" horizontally and vertically). They're identically accurate in every way. But obviously you don't know this. You haven't shot 'em yet.
You do what many shooters do. Take 3 rounds of one, shoot 'em, then take 3 rounds of the other and shoot them too. You then measure your group in MOA.
We can be pretty confident that one group will be smaller than the other by pure random chance. But does that mean that one is actually 'better'?
No, it does not.
Let's look at the distribution curves again. Let's say that for load #1 the three rounds you shot landed within 1SD of the mean. This is pretty likely. You've got a 68% chance of that happening so with only 3 shots in the group the odds are in your favor. That load posts a group of MAX 1" or 1MOA. You're pretty happy and you go hunting. Let's say for load #2 the three you randomly picked to shoot land within 2SD of the mean. You've got a 95% chance of that happening. The second load therefore gives a group of 2" or 2MOA. Twice what the first load gave you.
Obviously based on this you go shoot with load #1, boasting happily to your buddies at the bar about your 'sub-MOA' rifle.
But the two groups were equally accurate. If you performed the same test again, the results could completely flip the other way based on pure random chance. You've learned nothing.
And that sub-MOA rifle? It's not even a 1.5MOA rifle. The standard distribution tells us that actually, if you fire 20 shots, your group is actually barely keeping under 2MOA. If you fire 100 rounds of that load over the following year, the actual group is more like 3MOA... ponder that next time you have a 'flier'.
It's the same story when people say their rifle 'likes' or 'doesn't like' a specific brand of ammo based on only a few shots, or pick a specific bullet because it's 'way more accurate'. Maybe it is, maybe it isn't. You don't know and you've done nothing to find out. You've just cherry picked a group of a few shots that happened to fall in the 68% confidence interval instead of the 95% confidence interval. It means nothing.
That brings us onto Topic 2 - What can be done?
So, we know from the above that using a small number of shots cannot accurately and truthfully distinguish between two loads in terms of their grouping. What can we do instead? Well adding more rounds to your group starts to give you a truer picture of what is going on, but ammo is expensive and no one wants to be sat at the bench doing load development and shooting 20 rounds of each load in a ladder test. Your barrel wouldn't last long either.
We have to be pragmatic here. We must accept that actually, you will never be able to find the 'true' best load. But we can truthfully and accurately understand what a load is doing and if it is good enough for our purposes.
I am proposing the following method to achieve that. It is not without its drawbacks, but it will be far more statistically robust. I welcome criticism and feedback.
Step 1. Choose a bullet, any bullet. You'll never know if it's the 'most accurate' so pick one you like, one whose performance you trust, one that is readily available and in budget. Stick with it.
Step 2. Do the same with powder and all other components. Again, you don't know 'the best' and you never will, but you can choose one you can source and I'll share a method later to see if it's 'good enough'.
Step 3. Choose a velocity. What energy do you want, do you have a figure in mind, a goal you'd like to meet or a speed that seems reasonable based on your loading data?
Step 4. Ladder test. 1 round of each powder charge. No worries about accuracy, testing purely for a charge to meet your velocity. Define your powder charge when you chrono the velocity you want.
Step 5. You now have your load. But is it 'acceptably' accurate? Load 25x bullets of this load. Use 5 to zero the rifle. Get a target with a clear and defined center point. Shoot all 20 rounds at the target, measuring the velocity as you go. First sense check. What is your velocity SD like, are you hitting your target energy? Second sense check. Go to your target and measure distance from the center of the target (which as you zeroed should be center of the group) to the center of each bullet hole. Write down all 20 measurements. Enter these into the SD calculator above to get your SD for the load.
Step 6. You now have a mean (0,0) and an SD. As such, you can say (with actual confidence) how accurate the load is. For instance, if your SD is 0.2", you can say with certainty that 99.7% of all rounds from that group fall within 0.6" of the aim point (1.2MOA overall). If the SD is 0.5", 99.7% of all rounds of that loading will fall within 1.5" of your aim point (3MOA overall). Is this accurate enough for what the rifle and load is intended to do?
Bear in mind that this is the 99.7% interval, most rounds will be closer than this (3MOA at 99.7% means that 68% of shots fall within 1MOA and 95% fall within 2MOA. That's minute of deer in my book, especially if your annual hunting round count is only 20 rounds of so).
If it is, you have a load. If it isn't, choose a variable at random (bullet, powder charge etc), change it and try steps 5 + 6 again. I think you'll find pretty quickly if you have an actually 'bad' bullet, velocity etc for the rifle, and actually, in most cases the method above will be 'adequate' in just one go.
So there you go. A load development strategy that is a. statistically valid and b. uses no more ammo than just shooting random 3 round groups and cherry picking something for no good reason. Heck, it might even save you time and money pointlessly shooting random load combinations to learn nothing until you get lucky with one random load that happens to throw out a small group through random chance.
Thoughts? I bet there are other (and better) statisticians on this forum than I, so please chime in!
I've been meaning to put something together on this topic for a while as it's a persistent blind spot within the shooting and reloading community. @Shooter375 s recent thread on crimping finally gave me the incentive to put words to forum. Not calling him out specifically, just the latest in a long line of threads on reloading, grouping and what it all means. I think this'll be of interest to a few of our members and may spark some lively discussion.
This post will be long, and will be split into 2 main topics:
1. Basic statistics and why 3 round group don't mean anything. This'll be math heavy (dull, I know!), but should be mildly interesting and give sufficient background for it all to make sense.
2. If 3 round groups mean nothing, then what can we do instead to guide load development? This section will be more practical and maybe it'll save people some time and money.
Here we go!
Topic 1 - Stats 'n' stuff.
This is a normal distribution curve:
Scary, I know. But it's a surprisingly useful thing. What this curve does, is explain the distribution of data points within a sample using 2 main criteria. These are; the mean of the data set, and the standard deviation (SD). I will not go into the math of what SD is, but this link is here for those who are interested: https://www.mathsisfun.com/data/standard-deviation.html
This calculator allows you to calculate SD from a data set: https://www.calculator.net/standard-deviation-calculator.html
We'll get onto that later. Use 'Sample', not 'Population'.
This curve assumes something called 'normal' or Gaussian distribution. It assumes that data is spread about the mean in a specific way, with no skew to the high end, or the low end. Not all data does this, but normal distribution is called 'normal' for a reason. It is incredibly common in nature, and in complex systems. Examples of data that follow this trend include; height of people within a population, IQ in a population, torque applied to a bolt by a torque wrench, and roughly 90% of all other examples that spring to mind. Some topical ones for us on this forum might include bullet weights within a single box of bullets or velocity of a given load.
The curve actually tells us quite a lot about the data and helps us make conclusions. The mean tells us the mid point, whilst the standard deviation tells us how spread out that data is about the mean. A small SD suggests that all data points are tightly clustered, giving a steeper curve. You'll notice in the above that we have lines at -3, -2, -1, 0 and so forth. Each of these describes one standard deviation, and as the figure shows, we can make clear statements about what percent of our data points fit within a certain number of SDs from the mean.
As an example, Let's say you buy a box of shiny 300gr bullets. You weigh 20 of 'em, stick the values into the calculator above. You find that the mean is 300gr and the SD is 2gr. This tells us that in your box of 100 bullets, 68 of them weigh between 298 and 302gr, 95 of them weigh between 296 and 304gr, and all 100 of them weigh between 294gr and 306gr. 20 bullets (the sample) tells you enough about the entire box (population) to say this with confidence (real, statistical confidence, not the usual bollocks shooters say!)
Cool stuff, but why should you care?
Well, as with most complex systems, the grouping of a given load also follows this normal distribution. That's unsurprising. A rifle and its load is a complex system, made up of a whole lot of variables which themselves follow normal distributions. Bullet weight. Bullet diameter. Neck tension. Case volume. Specific energy of powder. Powder charge. Primer energy. All have a mean that they vary about randomly following the distribution above.
We can therefore imagine the group of a rifle to look something like this if you fired say 1000 rounds:
You have a normal distribution for 'x' (horizontal dispersion) and a normal distribution for 'y' (vertical dispersion) with the height of the little hill at any given (x,y) defining the relative number of those 1000 rounds that fall there. The middle of the hill would have coordinates 0,0 as it is 0" away from the center of the group both vertically and horizontally. You'll see that most rounds fall in the middle (mean +/-1 SD) but that some rounds fall further from the center at 2 or even 3 SD away from the mean center of the group.
So now you know what your group is doing, but what does it have to do with 3 round groups?
Well, let's say you have 2 loads, both of which have exactly the same mean (0,0) and the same SD (let's say 0.5" horizontally and vertically). They're identically accurate in every way. But obviously you don't know this. You haven't shot 'em yet.
You do what many shooters do. Take 3 rounds of one, shoot 'em, then take 3 rounds of the other and shoot them too. You then measure your group in MOA.
We can be pretty confident that one group will be smaller than the other by pure random chance. But does that mean that one is actually 'better'?
No, it does not.
Let's look at the distribution curves again. Let's say that for load #1 the three rounds you shot landed within 1SD of the mean. This is pretty likely. You've got a 68% chance of that happening so with only 3 shots in the group the odds are in your favor. That load posts a group of MAX 1" or 1MOA. You're pretty happy and you go hunting. Let's say for load #2 the three you randomly picked to shoot land within 2SD of the mean. You've got a 95% chance of that happening. The second load therefore gives a group of 2" or 2MOA. Twice what the first load gave you.
Obviously based on this you go shoot with load #1, boasting happily to your buddies at the bar about your 'sub-MOA' rifle.
But the two groups were equally accurate. If you performed the same test again, the results could completely flip the other way based on pure random chance. You've learned nothing.
And that sub-MOA rifle? It's not even a 1.5MOA rifle. The standard distribution tells us that actually, if you fire 20 shots, your group is actually barely keeping under 2MOA. If you fire 100 rounds of that load over the following year, the actual group is more like 3MOA... ponder that next time you have a 'flier'.
It's the same story when people say their rifle 'likes' or 'doesn't like' a specific brand of ammo based on only a few shots, or pick a specific bullet because it's 'way more accurate'. Maybe it is, maybe it isn't. You don't know and you've done nothing to find out. You've just cherry picked a group of a few shots that happened to fall in the 68% confidence interval instead of the 95% confidence interval. It means nothing.
That brings us onto Topic 2 - What can be done?
So, we know from the above that using a small number of shots cannot accurately and truthfully distinguish between two loads in terms of their grouping. What can we do instead? Well adding more rounds to your group starts to give you a truer picture of what is going on, but ammo is expensive and no one wants to be sat at the bench doing load development and shooting 20 rounds of each load in a ladder test. Your barrel wouldn't last long either.
We have to be pragmatic here. We must accept that actually, you will never be able to find the 'true' best load. But we can truthfully and accurately understand what a load is doing and if it is good enough for our purposes.
I am proposing the following method to achieve that. It is not without its drawbacks, but it will be far more statistically robust. I welcome criticism and feedback.
Step 1. Choose a bullet, any bullet. You'll never know if it's the 'most accurate' so pick one you like, one whose performance you trust, one that is readily available and in budget. Stick with it.
Step 2. Do the same with powder and all other components. Again, you don't know 'the best' and you never will, but you can choose one you can source and I'll share a method later to see if it's 'good enough'.
Step 3. Choose a velocity. What energy do you want, do you have a figure in mind, a goal you'd like to meet or a speed that seems reasonable based on your loading data?
Step 4. Ladder test. 1 round of each powder charge. No worries about accuracy, testing purely for a charge to meet your velocity. Define your powder charge when you chrono the velocity you want.
Step 5. You now have your load. But is it 'acceptably' accurate? Load 25x bullets of this load. Use 5 to zero the rifle. Get a target with a clear and defined center point. Shoot all 20 rounds at the target, measuring the velocity as you go. First sense check. What is your velocity SD like, are you hitting your target energy? Second sense check. Go to your target and measure distance from the center of the target (which as you zeroed should be center of the group) to the center of each bullet hole. Write down all 20 measurements. Enter these into the SD calculator above to get your SD for the load.
Step 6. You now have a mean (0,0) and an SD. As such, you can say (with actual confidence) how accurate the load is. For instance, if your SD is 0.2", you can say with certainty that 99.7% of all rounds from that group fall within 0.6" of the aim point (1.2MOA overall). If the SD is 0.5", 99.7% of all rounds of that loading will fall within 1.5" of your aim point (3MOA overall). Is this accurate enough for what the rifle and load is intended to do?
Bear in mind that this is the 99.7% interval, most rounds will be closer than this (3MOA at 99.7% means that 68% of shots fall within 1MOA and 95% fall within 2MOA. That's minute of deer in my book, especially if your annual hunting round count is only 20 rounds of so).
If it is, you have a load. If it isn't, choose a variable at random (bullet, powder charge etc), change it and try steps 5 + 6 again. I think you'll find pretty quickly if you have an actually 'bad' bullet, velocity etc for the rifle, and actually, in most cases the method above will be 'adequate' in just one go.
So there you go. A load development strategy that is a. statistically valid and b. uses no more ammo than just shooting random 3 round groups and cherry picking something for no good reason. Heck, it might even save you time and money pointlessly shooting random load combinations to learn nothing until you get lucky with one random load that happens to throw out a small group through random chance.
Thoughts? I bet there are other (and better) statisticians on this forum than I, so please chime in!
